How many sig figs in 400 – How many significant figures in 400? Embark on a captivating journey to unravel the secrets of significant figures, their importance in scientific measurements, and how they shape our understanding of the world around us. Join us as we delve into the fascinating realm of numbers and explore the intriguing case of 400, revealing the secrets it holds.
Significant figures, the backbone of scientific measurements, play a pivotal role in ensuring accuracy and precision. They guide us in expressing numbers with the appropriate level of certainty, enabling us to make informed decisions and draw meaningful conclusions from experimental data.
Understanding significant figures is not merely an academic exercise; it’s a key to unlocking the mysteries of the universe and making sense of the world we inhabit.
Overview of Significant Figures
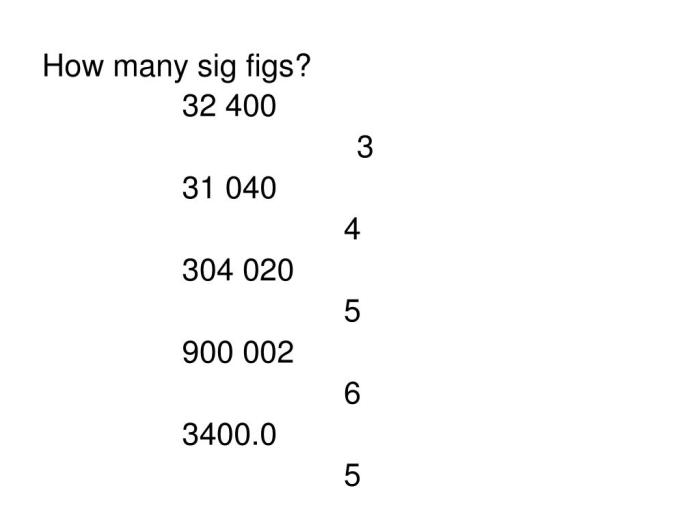
Significant figures, also known as significant digits, are the digits in a measured value that are known with certainty, plus one uncertain digit. They are important in scientific measurements because they indicate the precision and accuracy of the measurement.
For example, the number 12.34 has three significant figures, because the digits 1, 2, and 3 are known with certainty, and the digit 4 is uncertain. The number 0.0012 has two significant figures, because the digits 1 and 2 are known with certainty, and the digits 0 are placeholders.
400 has two significant figures. If you’re curious about words with “naut” in them, check out this list of words with naut in them . Back to our original topic, 400 has two significant figures because the zeros are placeholders.
Rules for Determining Significant Figures
- All non-zero digits are significant.
- Zeros between non-zero digits are significant.
- Zeros at the beginning of a number are not significant.
- Zeros at the end of a number that is written in decimal notation are significant.
- Zeros at the end of a whole number that is not written in decimal notation are not significant.
Determining Significant Figures in ‘400’

To determine the significant figures in the number ‘400’, we need to understand the rules for identifying significant figures in whole numbers.
Rules for Identifying Significant Figures in Whole Numbers
- All non-zero digits are significant.
- Zeros between non-zero digits are significant.
- Leading zeros (zeros to the left of the first non-zero digit) are not significant.
- Trailing zeros (zeros to the right of the last non-zero digit) are significant only if the number contains a decimal point.
Explanation of Significant Figures in ‘400’
Applying these rules to the number ‘400’, we can determine that it has only 1 significant figure. This is because:
- The digit ‘4’ is non-zero, so it is significant.
- The zeros ’00’ are trailing zeros, and since the number does not contain a decimal point, they are not significant.
Therefore, the number ‘400’ has 1 significant figure, which is the digit ‘4’.
Examples of Significant Figures in Different Numbers

To solidify our understanding of significant figures, let’s delve into specific examples that illustrate how they are determined in various numbers.
Table of Significant Figures
Below is a comprehensive table showcasing examples of numbers with varying significant figures:
| Number | Significant Figures | Explanation |
|---|---|---|
| 100 | 1 | Only the ‘1’ is a non-zero digit, making it the only significant figure. |
| 123 | 3 | All three digits are non-zero, resulting in three significant figures. |
| 1000 | 1 | The trailing zeros are placeholders and do not indicate significant figures. |
| 123.00 | 4 | The zeros after the decimal point are significant because they define the precision of the measurement. |
| 0.0012 | 3 | Leading zeros are not significant, but the non-zero digits ‘1’ and ‘2’ are. |
Applications of Significant Figures: How Many Sig Figs In 400

Understanding significant figures has practical applications in various scientific fields. It helps ensure accuracy in calculations, data analysis, and error analysis, leading to reliable and meaningful results.
Significance in Calculations
Significant figures guide the precision of mathematical operations. When multiplying or dividing numbers with different significant figures, the result should be reported with the same number of significant figures as the number with the least significant figures. This ensures that the precision of the calculation is not overstated.
Role in Error Analysis
Significant figures are crucial in error analysis. When measuring a quantity, the uncertainty associated with the measurement is expressed in terms of significant figures. By considering the significant figures in the measured values, scientists can determine the precision of their measurements and assess the potential error.
Examples in Scientific Experiments, How many sig figs in 400
In scientific experiments, significant figures are used to report experimental data accurately. For example, if the mass of a sample is measured to be 25.43 g, the result should be reported with four significant figures, indicating the precision of the measurement.
This information is essential for subsequent calculations and analysis.
Common Mistakes in Counting Significant Figures

Counting significant figures can be tricky, and it’s easy to make mistakes. Here are some of the most common errors students make:
1. Not counting zeros as significant figures
Zeros are only significant if they are between two non-zero digits. For example, the number 100 has two significant figures, while the number 0.01 has only one significant figure.
2. Counting trailing zeros as significant figures
Trailing zeros are not significant figures unless they are to the right of a decimal point. For example, the number 1000 has one significant figure, while the number 1000.00 has four significant figures.
3. Counting rounded numbers as having more significant figures than they actually do
When a number is rounded, it loses some of its significant figures. For example, the number 123.45 has five significant figures, but if it is rounded to 123, it only has three significant figures.
4. Confusing precision with accuracy
Precision refers to the number of significant figures in a measurement, while accuracy refers to how close a measurement is to the true value. It is possible to have a measurement that is precise but not accurate, or vice versa.
5. Not understanding the concept of significant figures
It is important to understand the concept of significant figures in order to count them correctly. Significant figures are the digits in a number that are known with certainty, plus one digit that is estimated. If you are not sure how to count significant figures, it is best to err on the side of caution and count fewer significant figures than you think you have.
Examples of Numbers Where Students Often Make Mistakes
- 100 (two significant figures)
- 0.001 (one significant figure)
- 123.456 (six significant figures)
- 123.00 (four significant figures)
- 123 (three significant figures)
FAQ Resource
What is the concept of significant figures?
Significant figures are the digits in a number that are known with certainty, plus one estimated digit. They provide a way to express the reliability of a measurement.
How do I determine the number of significant figures in 400?
400 has one significant figure because all the zeros are placeholders.
Why is it important to understand significant figures?
Significant figures help us to avoid reporting results with a false sense of precision. They ensure that we are only reporting the digits that we know with certainty.

